Neuronales Netz (Funktionsweise)
Contents
Neuronales Netz (Funktionsweise)¶
In diesem Abschnitt soll ein Einblick in den Aufbau und den Lernvorgang eines neuronalen Netzes geschaffen werden.
Verdeckte Schicht¶
Bisher hatten wir nur ein Neuron. Da ein neuronales Netz aus mehreren solcher Neuronen aufgebaut ist, befasst sich dieser Abschnitt damit, wie die einzelnen Neuronen zu einem Netz verknüpft werden können, wie diese Neuronen arbeiten und wie es das neuronale Netz schafft, etwas zu lernen.
Ein Netz aus mehreren Neuronen: Wir beginnen wieder mit einem einfachen Beispiel und verbinden ein paar Neuronen zu einem einfach NN:
Input Layer: X1, X2, X3, b
Hidden Layer Neuron 1, Neuron 2, Neuron 3
Output Layer Neuron 4
Beispiel:
X1: Anzahl Zylinder
X2: Leistung kw
X3: Gewicht kg
Die Neuronen verteilen sich selbst auf verschiedene Features auf. Jedes Neuron spezialisiert sich auf eine bestimmte Eigenschaft z.B.:
Neuron 1: Kleinwagen oder SUV (relevant: X1, X2, X3)
Neuron 2: Preis
Neuron 3: Beschleunigung (relevant: X2,X3)
Relevante Verbindungen werden vom Algorithmus verstärkt und nicht benötigte Verbindungen werden ignoriert (Gewicht wird sehr klein oder Null).
Der Output-Layer soll z.B. den Verbrauch vorhersagen und wird entsprechend jene Verbindungen verstärken, die besonders großen Einfluss auf den Verbrauch haben.
Die Aktualisierung der Gewichte hat einen großen Einfluss auf diesen Vorgang.
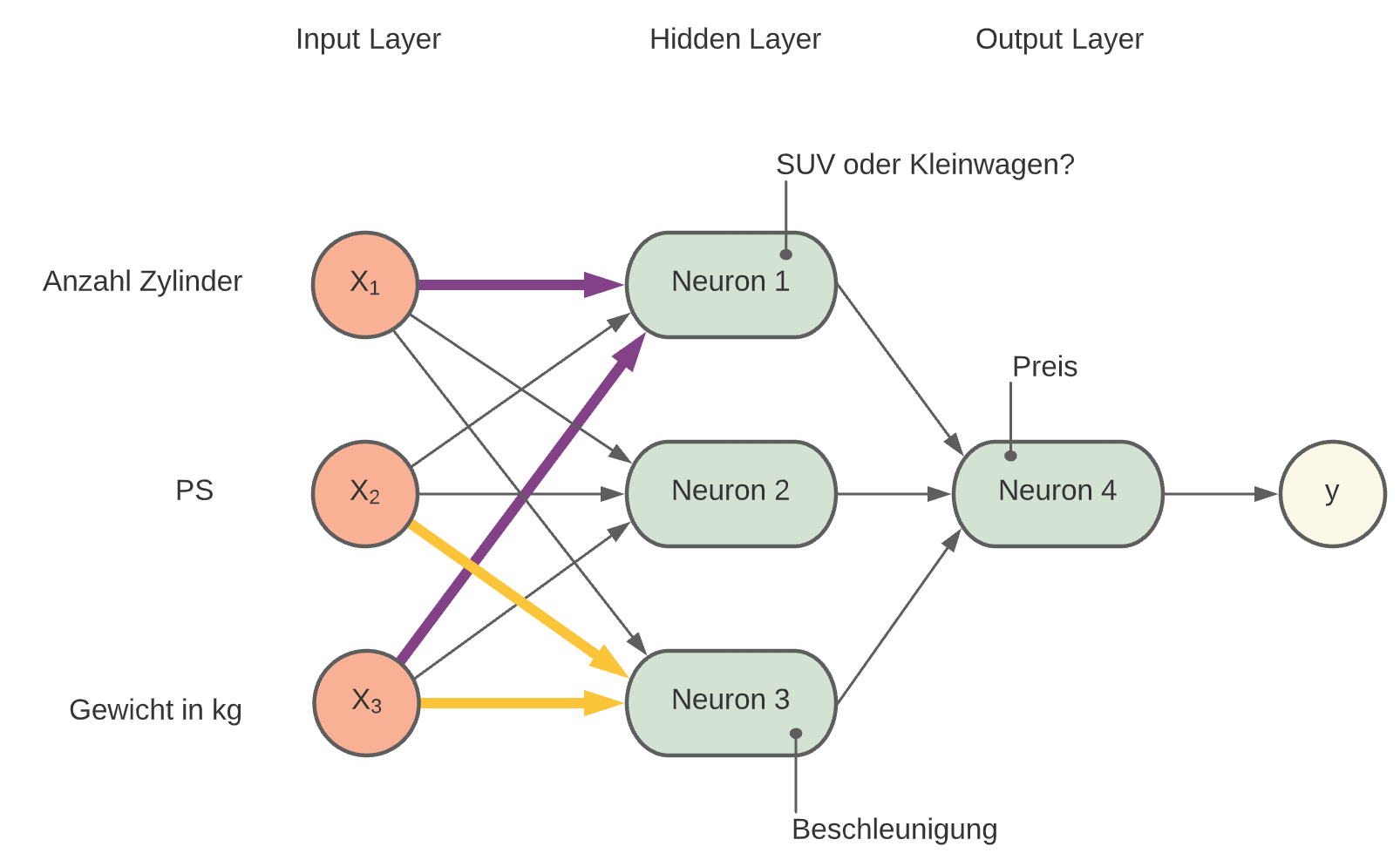
Fig. 8 zweilagiges-Neuronales Netz.¶
Weitere Informationen: Neural network architecture.
Note
Die Neuronen im Hidden Layer übernehmen jeweils verschiedene Hilfsaufgaben. Der Output Layer kombiniert der Ergebnisse aus dem Hidden Layer und gibt eine Vorhersage aus.
Note
Es gilt grundsätzlich:
Neuronale Netze mit einem beliebig großen Hidden-Layer können jede beliebige Funktion approximieren.
je mehr Knoten das Netz besitzt, desto genauer kann es die math. Funktionen annähern.
Gewichte aktualisieren¶
Nach der Initialisierung der Gewichte wird ein Ausgangswert berechnet. Passt dieser “Vorhersagewert” nicht zum richtigen Ergebnis, dann müssen die Gewichte dementsprechend angepasst werden, so dass das Ergebnis stimmt.
In der Abb.[Link] werden w1 und w2 so lange erhöht, bis der Vorhersagewert zum richtigen Wert passt.
Das Neuron gibt 0.5 aus, obwohl der richtige Wert 0.75 ist. Das bedeutet, das Modell ist noch nicht so gut an die Daten angepasst. Um das Modell den Daten besser anzupassen, stehen nur die Gewichte als Stellschrauben zur Verfügung und diese können nun stückweise erhöht werden bis das Modell die Daten ausreichend approximiert hat, siehe [Link].
Kostenfunktion¶
Die Aktualisierung der Gewichte wird mit Hilfe einer Kostenfunktion erreicht. Es gibt verschiedene Kostenfunktionen, eine davon ist die “quadratische Fehlerfunktion”.
Weitere Kostenfunktionen und Informationen hier.
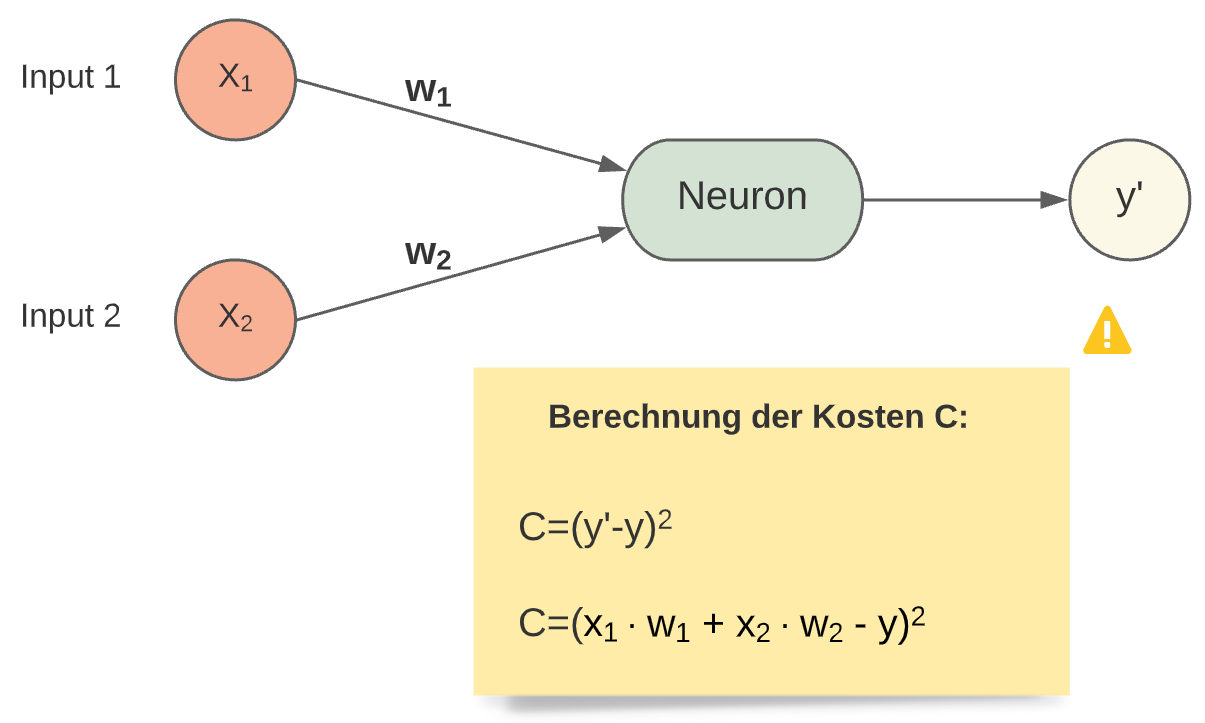
Fig. 9 Kostenfunktion¶
Das Quadrieren des Fehlers in der Kostenfunktion bewirkt eine viel größere Bestrafung für größere Fehler.
Werden nun wie üblich mehrere Datensätze trainiert, müssen die Gewichte nach jedem Datensatz angepasst werden, solange die Vorhersage vom wahren Wert y abweicht.
Die Abbildung dient nur zur Veranschaulichung. Im nächsten Abschnitt (Gradientenabstieg) wird gezeigt, wie die Kostenfunktion in Python minimiert wird.
Eine Kostenfunktion dient zum Minimieren des Fehlers. Man stellt eine Funktion auf, die den Fehler zwischen Schätzung und richtigem Wert berechnet und sucht dann die zugehörigen Gewichte, die den Fehler minimal werden lassen. Die Kosten C werden als Funktion der Gewichte formuliert. Da man es bei NN’s in der Regel mit komplexeren Funktionen und sehr vielen Gewichten zu tun hat, lässt sich das nicht mehr analytisch lösen. Für so einen Fall eignet sich das Gradientenabstiegsverfahren.
Gradientenabstieg¶
Wichtig zum Verständnis des Trainings von neuronalen Netzen.
Wie aktualisiert der Computer mehrere tausend Gewichte?
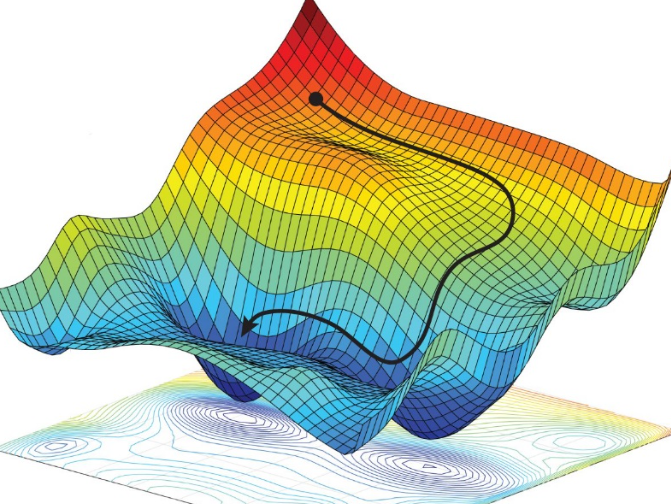
Mit dem Gradientenabstiegsverfahren wird Schritt für Schritt das Minimum einer Funktion gesucht. Bei einfachen Funktionen kann man das noch analytisch lösen, aber bei komplexeren Funtionen benötigt man das Gradientenabstiegsverfahren.
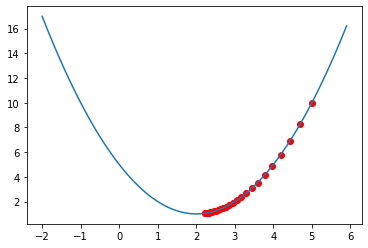
Wie findet man das Minimum bei komplexen Funktionen wie im Bild [Link]? Die Antwort lautet: Gradientenabstiegsverfahren. Das Verfahren wird anhand eines einfachen Beispiels näher erläutert.
import numpy as np
import matplotlib.pyplot as plt
def f(x):
return x ** 2 - 4 * x + 5
def f_ableitung(x):
return 2 * x - 4
x = 5
#Schrittweite bzw Lernrate (lr):
lr = 0.05
plt.scatter(x, f(x), c="r")
for i in range(0, 25):
steigung_x = f_ableitung(x)
x = x - lr * steigung_x
plt.scatter(x, f(x), c="r")
print(x)
xs = np.arange(-2, 6, 0.1)
ys = f(xs)
plt.plot(xs, ys)
plt.show()
4.7
4.43
4.186999999999999
3.9682999999999993
3.7714699999999994
3.5943229999999993
3.4348906999999995
3.2914016299999997
3.1622614669999995
3.0460353202999997
2.9414317882699996
2.847288609443
2.7625597484987
2.68630377364883
2.617673396283947
2.555906056655552
2.500315450989997
2.450283905890997
2.4052555153018975
2.364729963771708
2.328256967394537
2.2954312706550835
2.2658881435895752
2.239299329230618
2.215369396307556
Important
Man kann nun mit der Lernrate experimentieren und z.\(~\)B. einen großen Wert wählen. Es kann passieren, dass bei einer zu großen Schrittweite das Minimum übersprungen wird und somit nicht gefunden werden kann.
Gut zu wissen
In hochdimensionalen Räumen, spielen Probleme mit lokalen Minima kaum eine Rolle. Bei zwei und drei Dimensionen sind lokale Minima üblich. Bei einer Million Dimensionen sind lokale Minima selten. Die intuitive Erklärung ist, dass die Funktion, damit ein lokales Minimum existiert, in jeder Dimension gleichzeitig nach oben gekrümmt sein muss (erste Ableitung = 0, zweite Ableitung >= 0). Es macht Sinn, dass dies immer weniger wahrscheinlich wird, wenn weitere Dimensionen hinzugefügt werden, und bei einer Million Dimensionen ist es verschwindend unwahrscheinlich.
Was Sie anstelle lokaler Minima erhalten, sind Sattelpunkte, an denen sich einige Dimensionen nach oben und andere nach unten krümmen. Sattelpunkte können ebenfalls problematisch für die Optimierung sein, aber sie können mit ausgefallenen Optimierungstechniken behandelt werden.Quelle
Eine genauere Erklärung finden Sie unter Link
In der Praxis hat man es eher mit komplexeren Funktionen mit mehreren Minima zu tun. Die Gefahr, in einem lokalen Minimum stecken zu bleiben, ist in höher-dimensionalen Räumen zu vernachlässigen.
Stochastic Gradient Descent¶
Die Kosten für die gesamten Trainingsdaten zu berechnen und anschließend die Gewichte zu aktualisieren, würde bei sehr vielen Gewichten einen sehr hohen Rechenaufwand bedeuten, da die Kostenfunktion dann sehr viele variable Gewichte enthält. Deswegen geht man bei NN’s so vor, dass man nicht die Kosten für die gesamten Daten, sondern nur für den einzelnen Batch berechnet und somit die Kosten approximiert. Das macht man dann für alle Batches und aktualisiert nach jedem Batch die Gewichte. So werden die Gewichte pro kompletten Durchgang mehrmals aktualisiert und nicht nur einmal am Ende eines kompletten Durchgangs. Das bringt allerdings mit sich, dass die Gewichte hin und her springen, im „ZickZack zum Minimum laufen“, das führt insgesamt zu einem schnelleren Lernvorgang.
Begriffsdefinition:
Batch: Eine Gruppe von Trainingsdaten innerhalb des Datensatzes
Epoche: Alle Batches wurden einmal durchlaufen
Lernrate: Schrittgröße
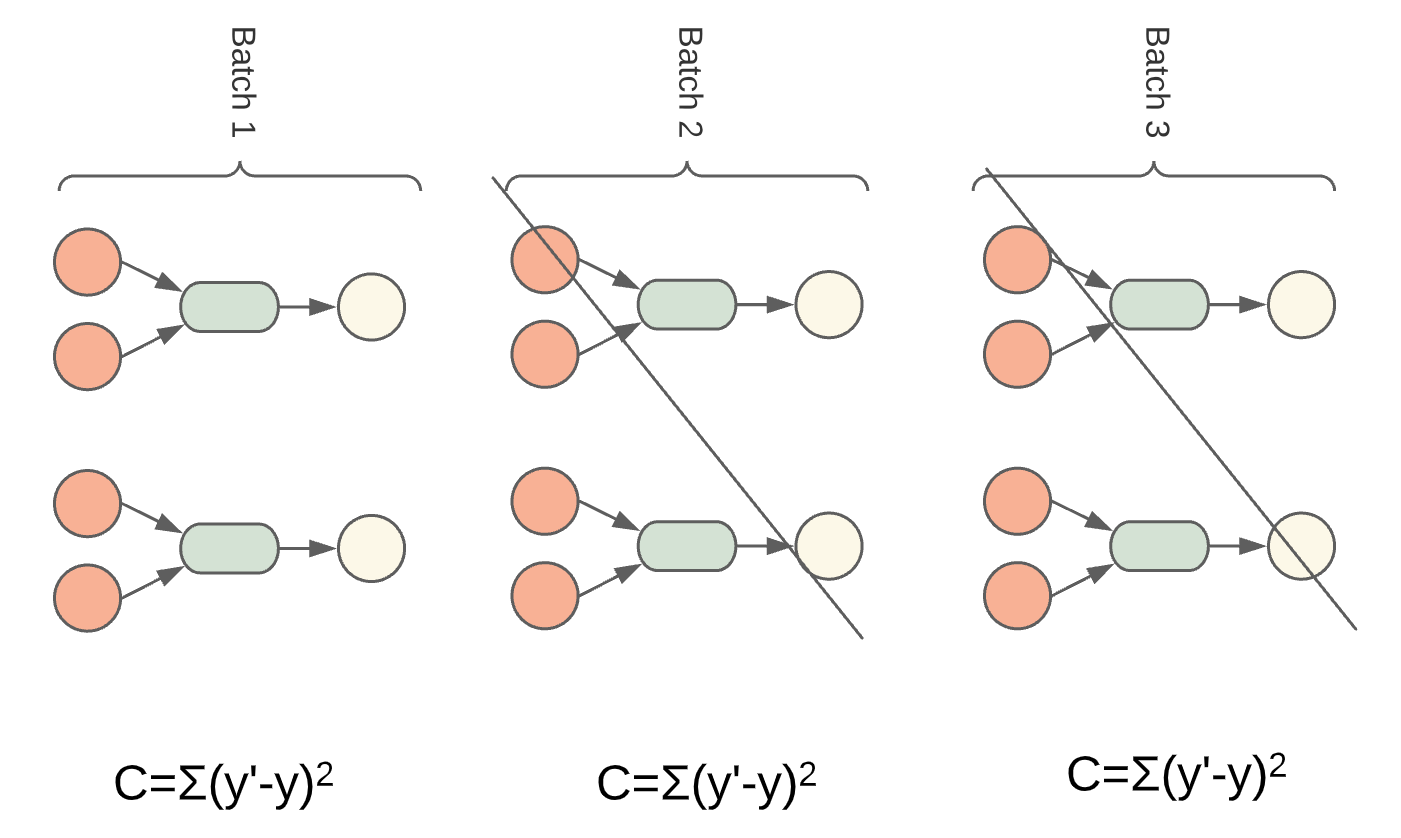
Fig. 11 erste Batch¶
Anstatt alle Gewichte mit einmal zu bestimmen, ist es vorteilhafter, den Trainingssatz in einzelne Batches aufzuteilen. Somit wird die Berechnung schneller und die Gewichte werden nach jedem Durchlauf angepasst.
Ablauf der Gewichtsanpassung für einen Batch:
Vorhersage machen
Kosten berechnen
Gewichte anpassen
dann nächste Batch
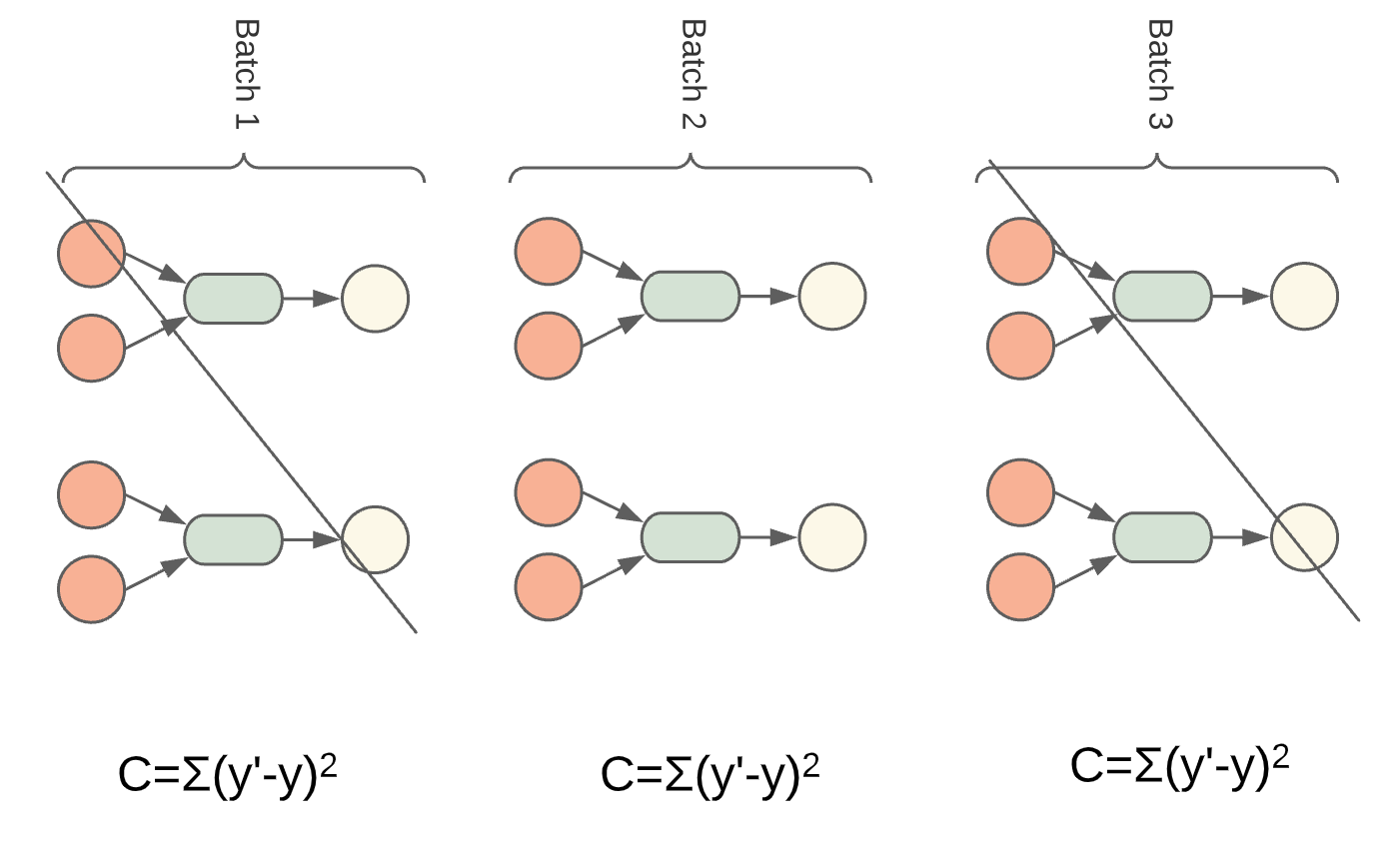
Fig. 12 Zweite Batch¶
Backpropagation¶
Problematik beim Lernen von mehrschichtigen NN’s:
Wie werden die Gewichte einer vorherigen Schicht aktualisiert?
Die Antwort lautet: Backpropagation!
Neuronale Netze wurden erst durch Backpropagation leistungsstark. Dadurch erst war es möglich, das gesamte neuronale Netz zu trainieren, also auch die vorherigen Schichten. Die Gewichte des gesamten NN werden immer wieder aktualisiert, solange bis der Vorhersagewert so nah wie möglich am gewünschten Wert liegt. Wie das genau gemacht wird, soll in diesem Abschnitt gezeigt werden.
verleiht den NN’s ihre Leistungsfähigkeit
verhalf zum Durchbruch von NN’s
Idee aus den 70ern
vorher konnte man nur Teile eines Netzes trainieren
Ein grobes, einfaches Beispiel zur Backward-Propagation:
Mit einem einfachen, groben Beispiel soll der Einstieg in das Verständnis der Backpropagation erleichtert werden. Für den Einstieg wird auf ein grobes Rechenbeispiel zurückgegriffen. Es soll an dieser Stelle zunächst nur der grobe Vorgang der Backward-Propagation veranschaulicht werden.
Es wird eine Vorhersage mit dem NN gemacht, diese Vorhersage \(\hat{y}\), weicht vom gewünschten / wahren Wert y ab
Die Abweichung e (Error) ist ein Maß dafür, wie stark die Vorhersage vom wahren Wert abweicht
Um die Abweichung zu minimieren, müssen nun die Gewichte aktualisiert werden
Der Fehler e=2 wird an die Ausgänge des Hidden-Layer transformiert:
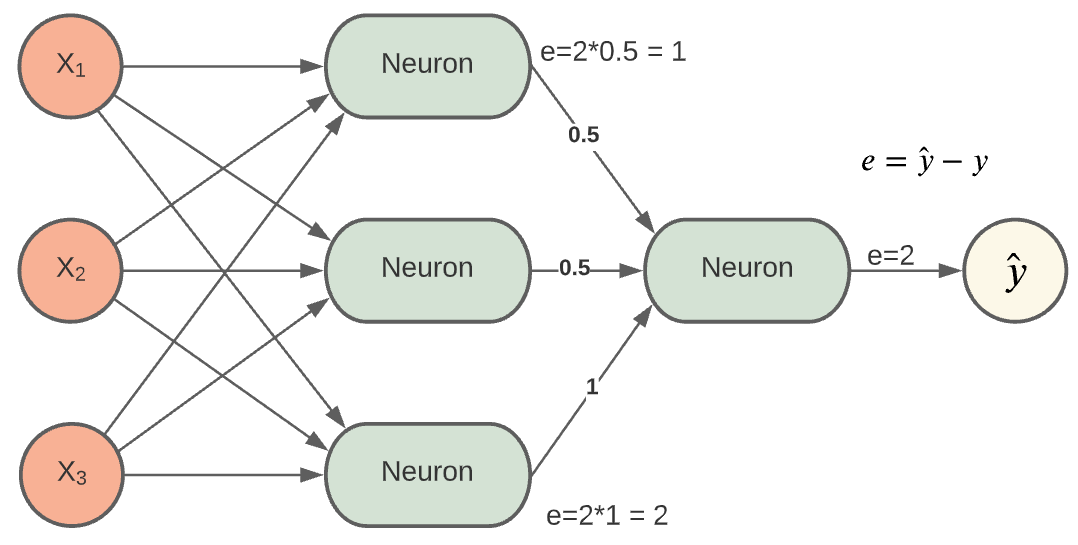
Fig. 13 Backpropagation¶
Initialisierung der Gewichte
Die Initialisierung kann darüber entscheiden, ob das NN trainieren kann oder nicht. Wie initialisieren wir die Gewichte? Mit null, wie im rechten Bild? Die Neuronen würden nur Nullen ausgeben. Das ergibt also keinen Sinn. Doch welche Werte sollte man am besten wählen? Weiterhin dürfen die Gewichte nicht alle mit den gleichen Werten initialisiert werden. Das ist auch aktiver Forschungsgegenstand, denn bei mehrschichtigen Netzen wird es umso wichtiger, die Gewichte „richtig“ bzw. nicht komplett falsch zu wählen. Besser ist es, den Gewichten unterschiedliche Werte zu geben. Das können zufällige, eher kleine Werte sein. So ist sichergestellt, dass jedes Neuron eine andere Funktion berechnet. Somit kann dann auch die Backpropagation richtig arbeiten und die Gewichte anpassen.
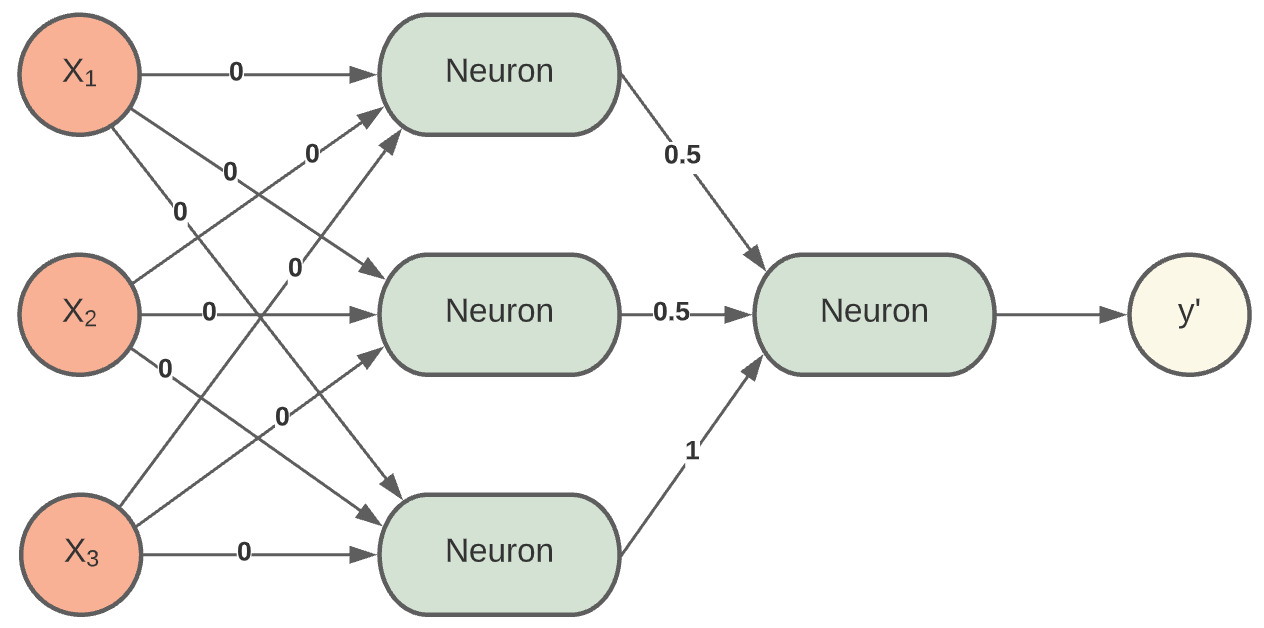
Fig. 14 Initialisierung der Gewichte¶
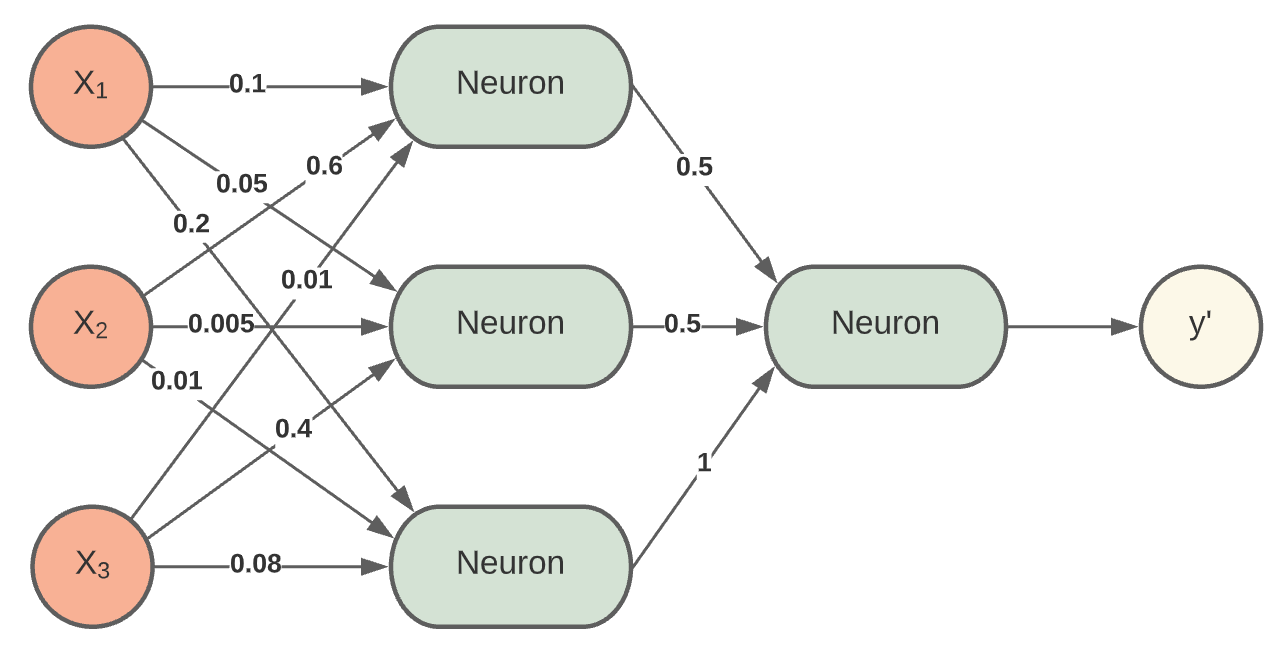
Fig. 15 Initialisierung der Gewichte mit kleinen Werten¶