Convolutional Neural Network
Contents
Convolutional Neural Network¶
Weshalb Convolutional Neural Networks? Das Hauptstrukturmerkmal von neuronalen Netzen ist, dass alle Neuronen miteinander verbunden sind. Wenn wir beispielsweise Bilder mit 28 x 28 Pixeln in Graustufen haben, haben wir am Ende 784 (28 x 28 x 1) Neuronen in einer Ebene, was überschaubar erscheint. Die meisten Bilder haben jedoch viel mehr Pixel und sind nicht grau skaliert. Unter der Annahme, dass eine Reihe von Farbbildern in 4K Ultra HD vorliegt, haben wir also 26.542.080 (4096 x 2160 x 3) verschiedene Neuronen, die in der ersten Schicht miteinander verbunden sind, was nicht wirklich handhabbar ist. Daher können wir sagen, dass neuronale Netze ohne Convolutional Layer, für die Bildklassifizierung nicht skalierbar sind. Insbesondere bei Bildern scheint es jedoch wenig Korrelation oder Beziehung zwischen zwei einzelnen Pixeln zu geben, es sei denn, sie liegen nahe beieinander. Dies führt zu der Idee von Convolutional Layers und Pooling Layers.
Ein Theorem aus dem Jahr 1988, das “Universal Approximation Theorem”, sagt, dass jede beliebige, glatte Funktion, durch ein NN mit nur einem Hidden Layer approximiert werden kann. Nach diesem Theorem, würde dieses einfache NN bereits in der Lage sein, jedes beliebige Bild bzw. die Funktion der Pixelwerte zu erlernen. Die Fehler und die lange Rechenzeit zeigen die Probleme in der Praxis. Denn um dieses Theorem zu erfüllen, sind für sehr einfache Netze unendlich viel Rechenleistung, Zeit und Trainingsbeispiele nötig. Diese stehen i.\(~\)d.\(~\)R. nicht zur Verfügung. Für die Bilderkennung haben sich CNNs als sehr wirksam erwiesen. Die Arbeitsweise soll in diesem Abschnitt erläutert werden. Der Grundgedanke bei der Nutzung der Convolutional Layer ist, dem NN zusätzliches „Spezialwissen“ über die Daten zu geben. Das NN ist durch den zusätzlichen Convolutional Layer in der Lage, spezielle Bildelemente und Strukturen besser zu erkennen.
Es werden meist mehrere Convolutional Layer hintereinander geschalten. Das NN kann auf der ersten Ebene lernen, Kanten zu erkennen. Auf weiteren Ebenen lernt es dann weitere “Bild-Features” wie z.\(~\)B. Übergänge, Rundungen o.\(~\)ä. zu erkennen. Diese werden auf höheren Ebenen weiterverarbeitet.
Beispiel einer einfachen 1D-Faltung:
Die beiden einfachen Beispiele sollen die Berechnung verdeutlichen. Die Filterfunktion wird auf die Pixel gelegt und Elementweise multipliziert. Im folgenden Beispiel werden 3 Pixel eines Bildes verwendet. Die Ergebnisse sagen etwas über den Bildinhalt aus:
positives Ergebnis: Übergang von hell zu dunkel
negatives Ergebnis: Übergang von dunkel nach hell
neutrales Ergebnis: Übergang wechselnd, hell-dunkel-hell oder dunkel-hell-dunkel
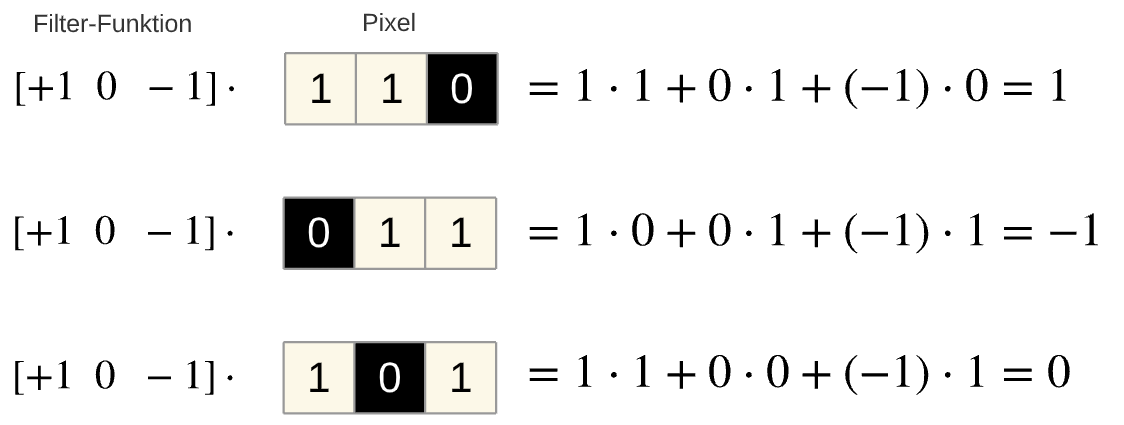
Fig. 16 Eindimensionale Faltung¶
Da ein Bild aus mehr als 3 Pixel besteht, muss die Filterfunktion über das gesamte Bild „geschoben“ werden. Das folgende Beispiel demonstriert den Vorgang der Convolution im Fall eines eindimensionalen Filters. Der Filter besteht in diesem Fall wieder aus einem Zeilenvektor mit 3 Elementen. Der Filter wird nun Pixelweise über die Bildzeile geschoben, die Ergebnisse werden gespeichert und geben wiederum Aufschluss über die Bildstruktur. Die Ergebnisse zeigen wieder die enthaltene Bildstruktur:
1: hell-dunkel
0: hell-dunkel-hell
0: dunkel-hell-dunkel
1: hell-dunkel –1: dunkel-hell

Fig. 17 Eindimensionale Faltung mit mehreren Übergängen¶
2-Dimensionale Faltung¶
In der Praxis werden in der Bilderkennung 2-dimensionale Filter verwendet, ein häufig verwendetes Format ist ein 3x3 Filter. Der Vorgang ist analog zum eindimensionalen Fall, der Filter wird über das gesamte Bild geschoben. Das folgende Beispiel zeigt einen Filter, der in der Lage ist, senkrechte Kanten zu erkennen.
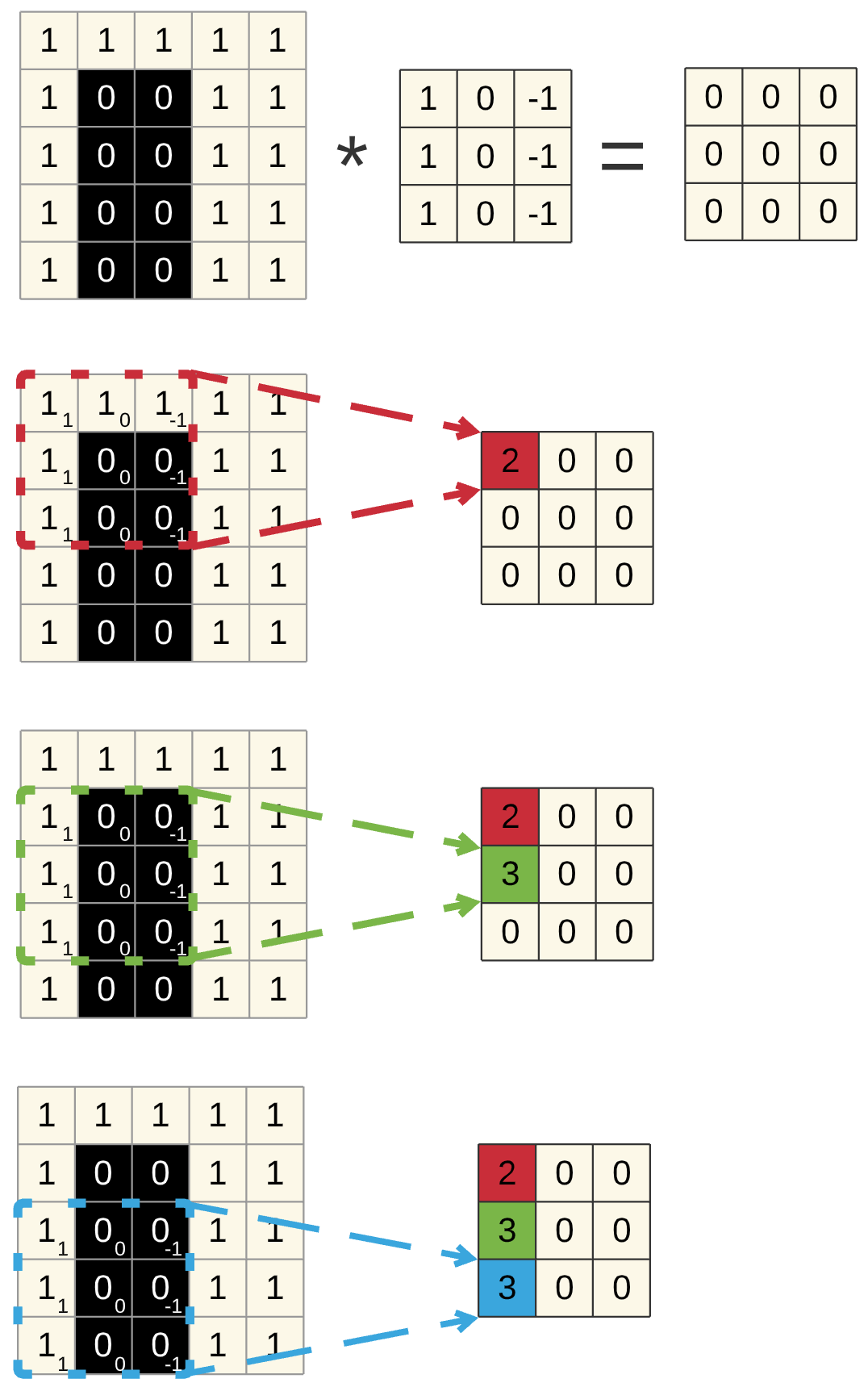
Fig. 18 Zweidimensionale Faltung Schrittweise¶
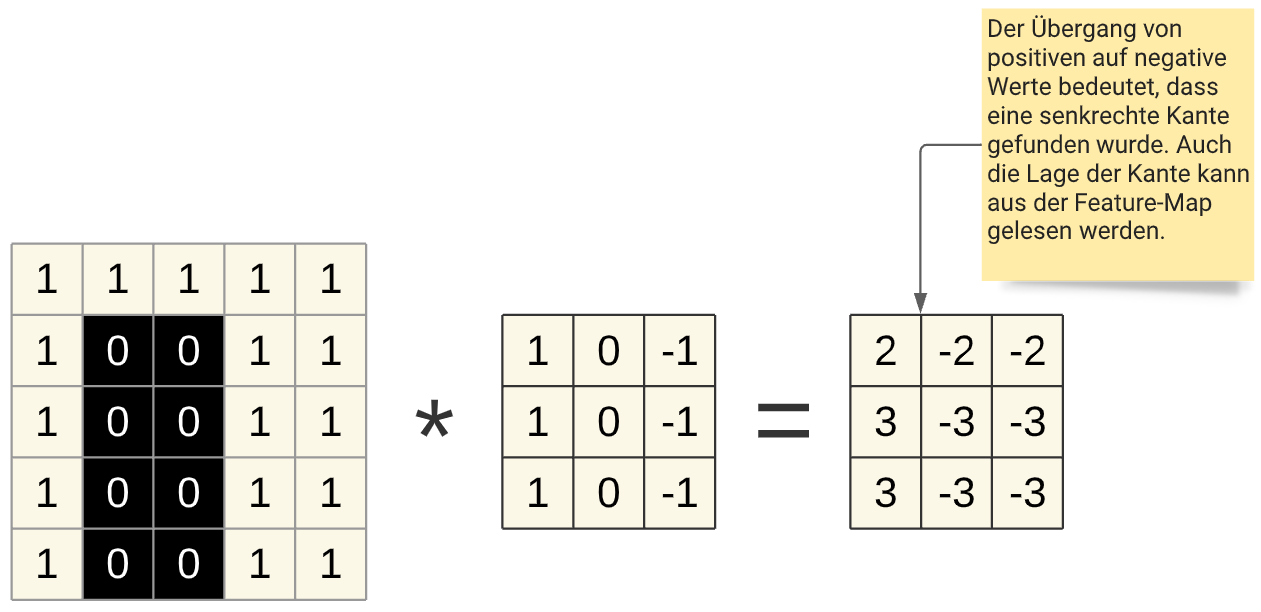
Fig. 19 Eindimensionale Faltung mit mehreren Übergängen¶
Die Werte der Filter bilden die Gewichte des Convolutional Layer. Diese Gewichte werden durch das Training selbst bestimmt und somit ist das CNN in der Lage, sich selbstständig auf relevante Features wie z.\(~\)B. Kanten zu fokussieren.
Im Folgenden noch weitere Ergebnisse für bestimmte Bildstrukturen:
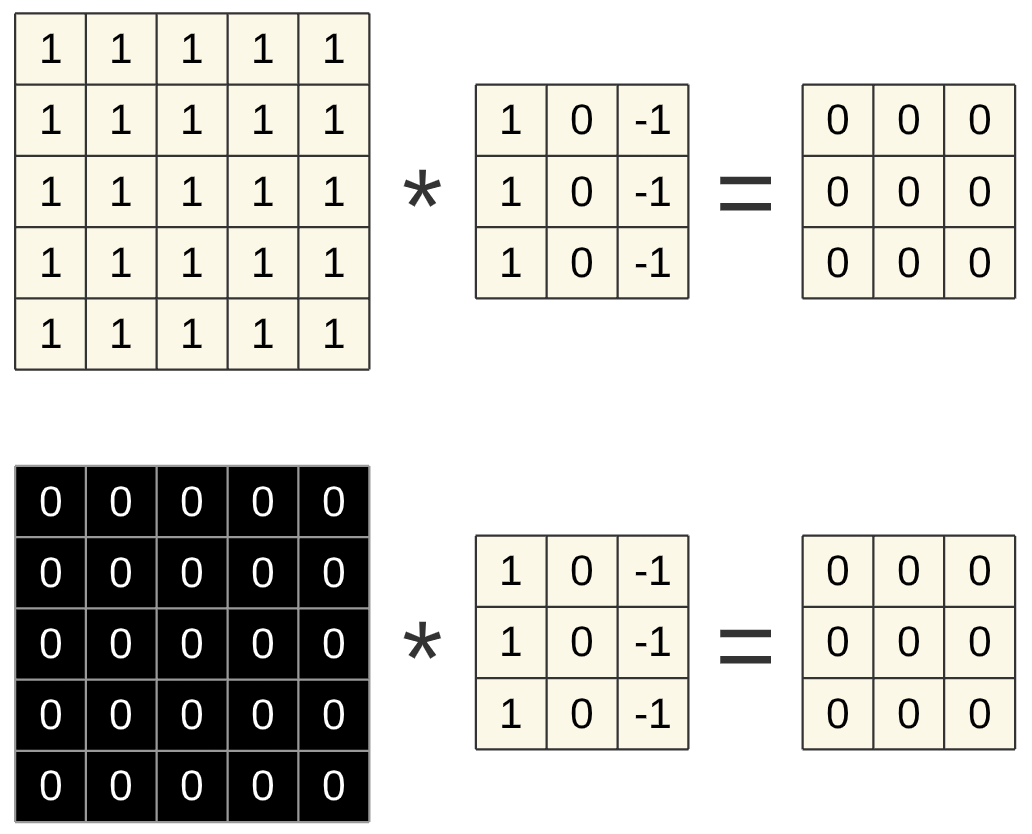
Fig. 20 Zweidimensionale Faltung einer einheitlichen Fläche¶
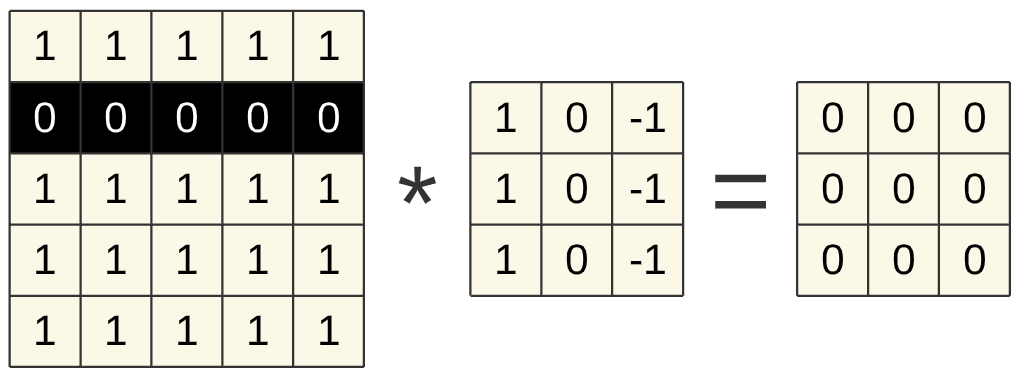
Fig. 21 Zweidimensionale Faltung horizontale Kante¶
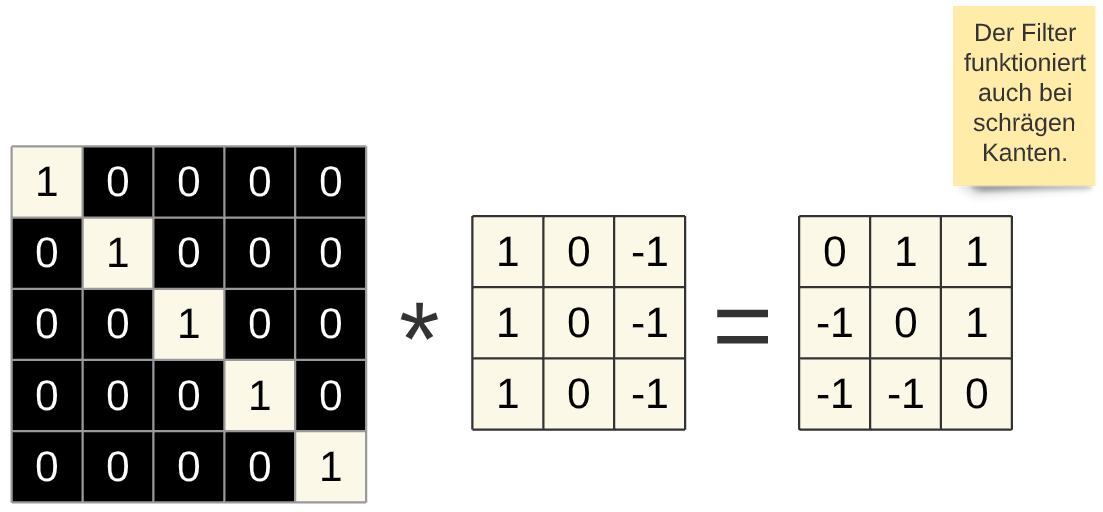
Fig. 22 Zweidimensionale Faltung schräge Kante¶
Mit Hilfe der Convolutional-Layer bekommt das neuronale Netz ein „Verständnis“ über die Struktur der Bilder (Ecken, Kanten, usw.) „eingebaut“. Das CNN ist somit auf die Erkennung von Bildern spezialisiert und dementsprechend leistungsfähiger als ein NN ohne dieses Bildverständnis.
Die Filter oder Kernels gibt man nicht vor, sondern lässt die Werte vom Convolutional Layer ermitteln. Die Kernels werden dabei so bestimmt, dass sie für die Erkennung der Bilder am effektivsten sind.
Es sollen aber nicht nur vertikale Kanten gefunden werden, sondern auch schräge und waagerechte. Da jeder Filter für ein bestimmtes Feature zuständig ist, benötigt das CNN mehrere solcher Filter, um alle relevanten Zusammenhänge extrahieren zu können. Die Anzahl an Filtern bereitgestellt werden sollten, hängt von den Daten ab und ist ein Hyperparameter den man empirisch ermitteln muss.
Convolutional Neural Net mit Keras¶
# Vorstellung: MNIST-Daten!
# http://yann.lecun.com/exdb/mnist/
# FashionMNIST: https://github.com/zalandoresearch/fashion-mnist
import gzip
import numpy as np
import numpy as np
from numpy import load
from tensorflow.keras.utils import to_categorical
X_train = load('../02_NN/Dataset/X_train.npy').astype(np.float32)#.reshape(-1, 784)
y_train = load('../02_NN/Dataset/y_train.npy')
#oh = OneHotEncoder()
#y_train_oh = oh.fit_transform(y_train.reshape(-1, 1)).toarray()
X_test=load('../02_NN/Dataset/X_test.npy').astype(np.float32)#.reshape(-1, 784)
y_test=load('../02_NN/Dataset/y_test.npy')
y_train = to_categorical(y_train)
y_test = to_categorical(y_test)
print(X_train.shape)
print(y_train)
(10500, 28, 28)
[[0. 0. 0. 0. 1.]
[1. 0. 0. 0. 0.]
[0. 1. 0. 0. 0.]
...
[0. 0. 1. 0. 0.]
[1. 0. 0. 0. 0.]
[0. 0. 0. 1. 0.]]
Das Format der Daten (10500, 28, 28) passt noch nicht zum geforderten Eingangsformat und muss angepasst werden. Das CNN verlangt ein vierdimensionales Array (10500, 28, 28, 1) und dieses wird mit der reshape-Methode erzeugt (siehe model.fit() im nächsten Programm).
Stochastic Gradient Descent
Das stochastische Gradientenabstiegsverfahren, wird mit optimizer=”sgd” ausgewählt.
# CNN!
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, Flatten
model = Sequential()
model.add(Conv2D(16, kernel_size=(3, 3), activation="relu", input_shape=(28, 28, 1)))
#model.add(Conv2D(32, kernel_size=(3, 3), activation="relu"))
model.add(Flatten())
model.add(Dense(5, activation="softmax"))
model.compile(optimizer="sgd", loss="categorical_crossentropy", metrics=["accuracy"])
model.fit(
X_train.reshape(10500,28,28,1),
y_train,
epochs=20,
batch_size=500)
Epoch 1/20
21/21 [==============================] - 1s 22ms/step - loss: 229.5953 - accuracy: 0.3178
Epoch 2/20
21/21 [==============================] - 0s 21ms/step - loss: 0.9440 - accuracy: 0.6190
Epoch 3/20
21/21 [==============================] - 0s 21ms/step - loss: 0.6530 - accuracy: 0.7649
Epoch 4/20
21/21 [==============================] - 0s 21ms/step - loss: 0.5013 - accuracy: 0.8199
Epoch 5/20
21/21 [==============================] - 0s 22ms/step - loss: 0.4058 - accuracy: 0.8393
Epoch 6/20
21/21 [==============================] - 0s 22ms/step - loss: 0.4397 - accuracy: 0.8294
Epoch 7/20
21/21 [==============================] - 0s 22ms/step - loss: 0.3674 - accuracy: 0.8583
Epoch 8/20
21/21 [==============================] - 0s 22ms/step - loss: 0.3386 - accuracy: 0.8624
Epoch 9/20
21/21 [==============================] - 0s 22ms/step - loss: 0.3027 - accuracy: 0.8836
Epoch 10/20
21/21 [==============================] - 0s 24ms/step - loss: 0.3147 - accuracy: 0.8754
Epoch 11/20
21/21 [==============================] - 0s 22ms/step - loss: 0.2679 - accuracy: 0.8914
Epoch 12/20
21/21 [==============================] - 0s 22ms/step - loss: 0.2448 - accuracy: 0.9017
Epoch 13/20
21/21 [==============================] - 0s 22ms/step - loss: 0.2369 - accuracy: 0.9060
Epoch 14/20
21/21 [==============================] - 0s 22ms/step - loss: 0.2150 - accuracy: 0.9114
Epoch 15/20
21/21 [==============================] - 0s 22ms/step - loss: 0.3123 - accuracy: 0.8828
Epoch 16/20
21/21 [==============================] - 0s 22ms/step - loss: 0.2253 - accuracy: 0.9091
Epoch 17/20
21/21 [==============================] - 0s 22ms/step - loss: 0.1853 - accuracy: 0.9243
Epoch 18/20
21/21 [==============================] - 0s 22ms/step - loss: 0.1935 - accuracy: 0.9216
Epoch 19/20
21/21 [==============================] - 0s 22ms/step - loss: 0.1948 - accuracy: 0.9217
Epoch 20/20
21/21 [==============================] - 0s 22ms/step - loss: 0.1432 - accuracy: 0.9435
<keras.callbacks.History at 0x7f180005d790>
RMSprop
Ein weiterer Optimizer ist der RMSprop. Dieser wird durch optimizer=”rmsprop” ausgewählt.
# CNN!
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, Flatten
model = Sequential()
model.add(Conv2D(16, kernel_size=(3, 3), activation="relu", input_shape=(28, 28, 1)))
model.add(Flatten())
model.add(Dense(5, activation="softmax"))
model.compile(optimizer="rmsprop", loss="categorical_crossentropy", metrics=["accuracy"])
model.fit(
X_train.reshape(10500,28,28,1),
y_train,
epochs=20,
batch_size=500)
Epoch 1/20
21/21 [==============================] - 1s 22ms/step - loss: 242.0397 - accuracy: 0.4830
Epoch 2/20
21/21 [==============================] - 0s 22ms/step - loss: 63.1420 - accuracy: 0.6419
Epoch 3/20
21/21 [==============================] - 0s 21ms/step - loss: 27.1203 - accuracy: 0.7310
Epoch 4/20
21/21 [==============================] - 0s 22ms/step - loss: 10.0603 - accuracy: 0.8360
Epoch 5/20
21/21 [==============================] - 0s 22ms/step - loss: 4.6834 - accuracy: 0.8353
Epoch 6/20
21/21 [==============================] - 0s 21ms/step - loss: 2.2660 - accuracy: 0.8735
Epoch 7/20
21/21 [==============================] - 0s 22ms/step - loss: 1.4034 - accuracy: 0.9078
Epoch 8/20
21/21 [==============================] - 0s 22ms/step - loss: 0.9845 - accuracy: 0.9339
Epoch 9/20
21/21 [==============================] - 0s 22ms/step - loss: 0.5971 - accuracy: 0.9523
Epoch 10/20
21/21 [==============================] - 0s 22ms/step - loss: 0.0607 - accuracy: 0.9875
Epoch 11/20
21/21 [==============================] - 0s 22ms/step - loss: 0.4934 - accuracy: 0.9664
Epoch 12/20
21/21 [==============================] - 0s 22ms/step - loss: 0.0084 - accuracy: 0.9981
Epoch 13/20
21/21 [==============================] - 0s 22ms/step - loss: 0.6108 - accuracy: 0.9581
Epoch 14/20
21/21 [==============================] - 0s 22ms/step - loss: 0.0010 - accuracy: 0.9998
Epoch 15/20
21/21 [==============================] - 0s 22ms/step - loss: 3.7297e-04 - accuracy: 1.0000
Epoch 16/20
21/21 [==============================] - 0s 22ms/step - loss: 0.4393 - accuracy: 0.9813
Epoch 17/20
21/21 [==============================] - 0s 22ms/step - loss: 5.3599e-04 - accuracy: 1.0000
Epoch 18/20
21/21 [==============================] - 0s 23ms/step - loss: 2.5452e-04 - accuracy: 1.0000
Epoch 19/20
21/21 [==============================] - 0s 22ms/step - loss: 0.3049 - accuracy: 0.9837
Epoch 20/20
21/21 [==============================] - 0s 23ms/step - loss: 4.4494e-04 - accuracy: 1.0000
<keras.callbacks.History at 0x7f17e27e5e50>
2 Convolutional Layer
Einen weiteren Convolutional Layer verwenden:
# CNN!
from tensorflow.keras.models import Sequential
from tensorflow.keras.layers import Dense, Conv2D, Flatten
model = Sequential()
model.add(Conv2D(16, kernel_size=(3, 3), activation="relu", input_shape=(28, 28, 1)))
model.add(Conv2D(32, kernel_size=(3, 3), activation="relu"))
model.add(Flatten())
model.add(Dense(5, activation="softmax"))
model.compile(optimizer="rmsprop", loss="categorical_crossentropy", metrics=["accuracy"])
model.fit(
X_train.reshape(10500,28,28,1),
y_train,
epochs=20,
batch_size=500)
Epoch 1/20
21/21 [==============================] - 2s 96ms/step - loss: 21.6524 - accuracy: 0.6189
Epoch 2/20
21/21 [==============================] - 2s 95ms/step - loss: 0.8093 - accuracy: 0.8665
Epoch 3/20
21/21 [==============================] - 2s 95ms/step - loss: 0.4227 - accuracy: 0.8997
Epoch 4/20
21/21 [==============================] - 2s 94ms/step - loss: 0.1646 - accuracy: 0.9585
Epoch 5/20
21/21 [==============================] - 2s 98ms/step - loss: 0.0131 - accuracy: 0.9990
Epoch 6/20
21/21 [==============================] - 2s 96ms/step - loss: 0.2447 - accuracy: 0.9744
Epoch 7/20
21/21 [==============================] - 2s 96ms/step - loss: 0.0067 - accuracy: 0.9998
Epoch 8/20
21/21 [==============================] - 2s 95ms/step - loss: 0.0017 - accuracy: 1.0000
Epoch 9/20
21/21 [==============================] - 2s 118ms/step - loss: 0.0815 - accuracy: 0.9895
Epoch 10/20
21/21 [==============================] - 3s 127ms/step - loss: 0.0597 - accuracy: 0.9820
Epoch 11/20
21/21 [==============================] - 3s 127ms/step - loss: 0.0013 - accuracy: 1.0000
Epoch 12/20
21/21 [==============================] - 3s 126ms/step - loss: 3.9080e-04 - accuracy: 1.0000
Epoch 13/20
21/21 [==============================] - 3s 128ms/step - loss: 1.1759e-04 - accuracy: 1.0000
Epoch 14/20
21/21 [==============================] - 3s 127ms/step - loss: 0.0034 - accuracy: 0.9983
Epoch 15/20
21/21 [==============================] - 3s 126ms/step - loss: 0.1700 - accuracy: 0.9794
Epoch 16/20
21/21 [==============================] - 3s 125ms/step - loss: 2.5466e-04 - accuracy: 1.0000
Epoch 17/20
21/21 [==============================] - 3s 128ms/step - loss: 1.7362e-04 - accuracy: 1.0000
Epoch 18/20
21/21 [==============================] - 3s 132ms/step - loss: 6.7044e-05 - accuracy: 1.0000
Epoch 19/20
21/21 [==============================] - 3s 128ms/step - loss: 7.7813e-05 - accuracy: 1.0000
Epoch 20/20
21/21 [==============================] - 3s 132ms/step - loss: 0.0971 - accuracy: 0.9824
<keras.callbacks.History at 0x7f17e27a5150>
Die Schraubenkopfbilder können vom CNN sehr gut gelernt werden. Die Trainingsgenauigkeit beträgt bis zu 100 %. Das war zu erwarten, da die Bilder recht einfach zu unterscheiden sind und für ein CNN kein Problem darstellen sollten.
Im nächsten Abschnitt wird der Datensatz mit den echten Bildern verwendet.
